Modelo de las situaciones didácticas (parte II)

Marco Feria

 

La denominada escuela francesa de Didáctica de la Matemática “estudia las actividades que tienen por objeto la enseñanza, evidentemente en lo que tienen de específicas las matemáticas” (Brousseau, 1989, p. 135).

La Didáctica de la Matemática nació en los años setenta, a partir de las preocupaciones de un grupo de investigadores matemáticos, que centraron sus esfuerzos en aspectos epistemológicos, sociales y cognitivos de las diferentes interacciones entre el saber, los alumnos y el maestro, teniendo en cuenta el contexto particular del aula de clase. Los resultados de sus investigaciones generaron conceptos propios tales como: el contrato didáctico, el obstáculo epistemológico, la situación didáctica y la situación a-didáctica; con el propósito de descubrir e interpretar los fenómenos y los procesos ligados a la adquisición y a la transmisión del conocimiento matemático.

Dentro de esta didáctica, Brousseau (1986) plantea la Teoría de Situaciones en la enseñanza, en busca de las condiciones encaminadas a encontrar un origen simulado de los conocimientos matemáticos, partiendo de la hipótesis de que estos no se construyen de manera espontánea. Con esta teoría se estudian y modelan fenómenos didácticos que ocurren cuando un docente se propone enseñar una noción o un concepto que el alumno debe construir a partir de un conjunto de problemas.

Según Brousseau (1986), desde esta perspectiva, se establecen dos roles bien diferenciados. El primero se refiere al rol del matemático, cuya función consiste en comunicar sus resultados, identificando previamente lo que puede ser susceptible de convertirse en un saber nuevo que sea de interés para que otros (profesores) desarrollen una didáctica práctica que consiste en descontextualizar y despersonalizar el saber. Por el contrario, el segundo rol, se centra en el caso del maestro quien realiza el proceso inverso, a partir del saber, lo re-personaliza y lo re-contextualiza con el propósito de darle sentido a lo que enseña para convertirlo en conocimientos del alumno. Para ello, debe proponer situaciones de aprendizaje que guíen a los estudiantes desde una estrategia inicial hasta el logro de una acomodación de sus conocimientos en correspondencia con la situación propuesta, y de una manera más general. En este caso, si los estudiantes han aprendido, deben realizar también una labor de despersonalización y de re-descontextualización que les exigiría probar, construir modelos, lenguajes, conceptos; que al interactuar con el otro les permita su reconocimiento; y con base en ello asuman los aprendizajes que son útiles. En otras palabras, que los institucionalicen como un saber propio.

De igual forma, el rol del maestro, según Brousseau (1986), implica acciones como:

Escoger situaciones que implican hacer que los estudiantes las apropien y se sientan responsables de solucionarlas; luego, debe des-didactificar, para que el estudiante no haga solo aquello que el maestro quiere, sino que maneje las devoluciones de la situación; asimismo, debe guiar didácticamente las relaciones que se presentan (preguntas y respuestas); finalmente, debe institucionalizar tanto los saberes adquiridos como el sentido de los mismos para darles un status, y un reconocimiento al objeto de conocimiento para volverlo cultural y realizable (p. 6).

Este enfoque de la didáctica, el proceso de producción de conocimientos matemáticos se describe a partir de dos tipos básicos de interacción: la del alumno con una problemática que ofrece resistencias y la del docente con el alumno. Para realizarlo, Brousseau (citado en Pérez & Begoña, 1986), creó el concepto de contrato didáctico, definido como un conjunto de reglas, con frecuencia no enunciadas explícitamente, que establecen  las relaciones entre el contenido enseñado, con la participación de los alumnos y el profesor dentro de la clase de matemáticas. De tal forma que el aprendizaje de matemáticas no se reduce a recordar fórmulas, teoremas o definiciones para resolver problemas mediante la imitación de explicaciones impartidas por el profesor en la clase, o con apego a los métodos ilustrados en los textos escolares.

Esta teoría identificó varios tipos de situaciones o estados del contrato didáctico que permiten formar lo que es el tema general de una secuencia didáctica para provocar una idea artificial de los conceptos matemáticos. Estas situaciones podrían estar centradas en la acción, en la que los estudiantes hacen sus primeros intentos por resolver un problema propuesto por el profesor; quien los orienta hacia la comunicación, para socializar los resultados del trabajo con los compañeros. Otras situaciones están centradas en  la validación, para las cuales se deben presentar argumentaciones teóricas o empíricas (Brousseau, 1986).

En síntesis, entender y conocer los postulados, las características de los diferentes  enfoques referenciados en esta  reflexión,  que de una u otra forma  prevalecen  en los estudios e investigaciones que desarrollan los estudiantes de la maestría,  permite formular nuevos campos de estudio  y facilita el camino hacia futuras preguntas de investigación y por qué no decirlo, en la creación de un programa de investigación  con el propósito de  validar  dichas  teorías,  y  coadyuvar  con un valor  agregado en el cual la praxis pedagógica trascienda lo teórico y  permita construir otras tendencias teóricas en la forma como concebimos la didáctica de la educación matemática.

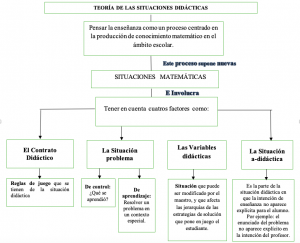
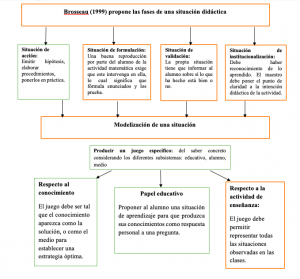
Los siguientes esquemas presentan las reflexiones anteriormente desarrolladas para comprender específicamente la teoría de las situaciones.

ESQUEMA: TEORIA DE LAS SITUACIONES    Seleccionado de Brousseau (1999)

 

 

 

_____________________

Referencias

Brousseau, G. (1986). Teoría de las situaciones didácticas. Grenoble, Francia: Ediciones El pensamiento salvaje.

Brousseau, G. (1988). Teoría de situaciones didácticas. Francia: Ediciones El pensamiento salvaje.

Brousseau, G. (1986). Fundamentos y métodos de la didáctica de las matemáticas. Publicado con el título.“ Fondements et méthodes de la didactiques des mathématiques, en la revista, Recherches en Didactique des Mathematiques, 7(2), 33. Traducido por Centeno, J; Melnado, B; Ramón, J.

Brousseau, G. (1999). Educación y Didáctica de las matemáticas. Educación Matemática, 12(1), 5-38.

Feria, M. (2007). Percepción espacial y geometría intuitiva: Propuesta de unidades didácticas. Bogotá, Colombia: Editorial Universidad Externado de Colombia.

Feria, M. (2006). Percepción espacial y geometría intuitiva: Una puerta de entrada al aprendizaje significativo. Bogotá, Colombia: Editorial Universidad Externado.